线性代数，特征值与矩阵的秩之间的关系，证明和求通解
线性代数，特征值与矩阵的秩之间的关系，证明和求通解
我们给出一道实例，通过例题来帮助理解
做题之前先审题，第一小题很容易就做出来了
题目给出了两个信息，第一个，是矩阵A有3个不同的特征值
由此可以得到矩阵A可以对角化，与对角矩阵P{λ1,λ2,λ3}相似
第二个条件，就是α3=α1+2α2
可以得到
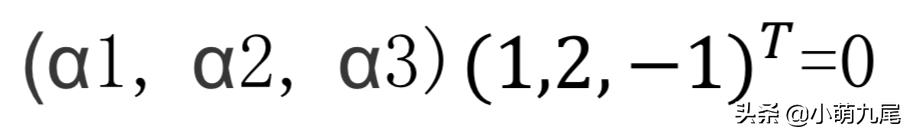
图二
由此可知，A的其中一个特征值便为0
由于三个特征值不同，说明其他两个特征值都不为零，那么它的对角矩阵P为{λ1,λ2,0}
因为相似，所以可以得到r(P)=r(A)=2
第二小题，要根据第一小题来做了
要求Ax=β的通解，我们先来看看Ax=0的通解
很明显，通过条件α3=α1+2α2可以得到Ax=0的通解，如下图所示
图三
再根据β=α1+α2+α3可以得到
图四
即为
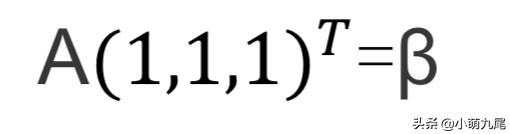
图五
那么最后就可以得到Ax=β的通解为
图六
详细解题过程如下图所示
图七，详细步骤如图
相关标签：
-
- 绵阳教育品牌名片-外国语学校
-
2025-03-17 06:32:17
-
- 惊：张馨予剪掉一身乌黑亮丽的长发，明星剪短发Tony成最大赢家！
-
2025-03-17 06:30:01
-
- 加强爱国主义教育 弘扬爱国主义精神
-
2025-03-17 06:27:46
-
- 关晓彤“缝纫机”造型《凤囚凰》开播，人物剧照抢先看，你追吗？
-
2025-03-17 06:25:31
-
- 中国国家地理：内蒙古高原
-
2025-03-17 06:23:16
-
- 文玩手串最新排行榜，不信你的就没上榜！
-
2025-03-17 06:21:00
-
- 王者荣耀历史战绩怎么查看 历史战绩查看方法
-
2025-03-17 06:18:45
-
- 黄子韬主演的剧版《大话西游》海报曝光，网友：烂片即视感
-
2025-03-17 06:16:30
-
- 二战德军经典冲锋枪：MP40冲锋枪
-
2025-03-17 06:14:15
-
- LOL新游戏模式“死兆星”介绍
-
2025-03-17 06:12:00
-
- 《锦绣未央》即将迎来大结局，跟着小编一起来剧透吧
-
2025-03-17 06:09:45
-
- 重庆出发，7月抢鲜价，特价机票343元起，已含税
-
2025-03-17 06:07:30
-
- 两千多万的一条蓝鳍金枪鱼有哪些功效？老师傅让各位收藏好
-
2025-03-17 06:05:14
-
- 春节回乡手记｜“三十晚上熬一宿”
-
2025-03-17 06:02:59
-
- 中央空调的男人你碰到过吗！中央空调等于渣男？
-
2025-03-17 06:00:44
-
- 妖艳女主甜文合集 ─ 只想看你脸红红
-
2025-03-17 05:58:29
-
- 男人腿毛少，说明什么？真正原因无非这个，看看你是否符合？
-
2025-03-17 05:56:14
-
- 康大飞卖掉有200W粉丝量的账号，原来独家创作者收益真的不多
-
2025-03-17 05:53:59
-
- WIFI无线网络突然变慢的问题有可能出在信道
-
2025-03-17 05:51:44
-
- 女人出轨的10种表现你是否注意到？
-
2025-03-16 14:01:22
《银河补习班》：马皓文对马飞的教育到底是成功的还是失败的？
又仙又美的72款平价纱裙半身裙来了，不管怎么穿都百搭